环球网校经济师人力资源专业初级考点预习

【考点二】算术平均数、几何平均数 #
(一)算数平均数的特点、适用范围
#
建议关注算术平均数的计算方法、几何平均数的用途。
|
定义 #
|
是全部数据的算术平均,又称均值,用 表示。 # |
|
特点 #
|
(1)是集中趋势最主要的测度值。 |
|
适用范围 # |
主要适用于数值型数据,但不适用于品质数据。 #
|
(二)两种算数平均数的比较 #
|
# |
简单算术平均数 # |
加权算术平均数 #
|
|
计算方法 #
|
设一组数据为X1,X2,…,Xn,计算公式为: #
# |
设原始数据被分成k组:各组的组中值为X1,X2,…,Xk,各组的频数分别为f1,f2,…,fk,计算公式为: # |
|
适用范围 #
|
用于处理未分组的原始数据 # |
用于处理经分组整理的数据 # |
【例如】某售货小组有5名营业员,元旦一天的销售额分别为520元、600元、480元、750元和500元,求该日每名营业员的平均销售额。 #
 #
#
【例如】某市商业企业协会根据100个会员样本,整理出一年销售额分布资料:
销售额分布资料
#
|
销售额(万元) # |
组中值 #
|
商业企业数fi # |
Xifi # |
|
100-150 #
|
125 #
|
4 # |
500 #
|
|
150-200 # |
175 # |
16 # |
2800 #
|
|
200-250 # |
225 #
|
40 # |
9000 # |
|
250-300 # |
275 # |
28 # |
7700 # |
|
300-350 #
|
325 #
|
10 #
|
3250 #
|
|
350-400 # |
375 # |
2 #
|
750 # |
|
合计 #
|
— # |
100 # |
24000 #
|
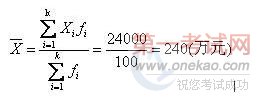 #
#
(三)几何平均数
1.n个观察值连乘积的n次方根就是几何平均数。
2.简单几何平均数的计算。 #
设一组数据为X1,X2,…,Xn,且大于0, 表示几何平均数,则: #
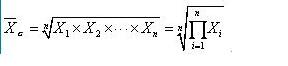
第二十一章 数据特征的测度
【考点一】众数、中位数
#
建议关注众数、中位数的计算方法。
(一)集中趋势的测度 #
集中趋势是指一组数据向某一中心值靠拢的倾向 #
(二)众数、中位数的计算方法、特点和应用范围 #
|
#
|
众数 # |
中位数 # |
|
计算方法 # |
一组数据中#p#分页标题#e#出现频数最多的那个数值,用M0表示 # |
把一组数据按从小到大的顺序进行排列,位置居中的数值叫作中位数,用Me表示。 #
#
|
|
特点 # |
是一个位置代表值,不受极端值的影响,抗干扰性强 # |
|
|
适用范围 # |
适用于品质数据、数值型数据 # |
主要用于顺序数据,也适用于数值型数据,但不适用于分类数据。 #
|
【考点二】数值型数据的整理与显示
#
建议关注数据的分组、数值型数据的图示。 #
(一)数据的分组
1.数据分组概述
|
定义 # |
是根据统计研究的需要,将数据按照某种标准划分成不同的组别。 # |
|
|
方法 # |
单变量值分组 # |
把每一个变量值作为一组。 |
|
组距分组 # |
将全部变量值依次划分为若干个区间,并将这一区间的变量值作为一组。 # |
|
2.组距分组的步骤 #
第一步,确定分组组数。
#
第二步,对原始资料进行排序。 #
第三步,求极差。将最大的观察值与最小的观察值相减便得到极差。 #
极差值=最大观察值-最小观察值 #
【例如】某组数据50、60、67、75、80、91、105、112中,极差值为?
极差值=最大观察值-最小观察值=112-50=62
#
第四步,确定各组组距。 #
(1)组距=极差/组数 #
(2)等距分组的情况下 ,最好把组距取成接近于能被5除尽的一个数。
(3)关系:组距与组数成反比关系。 #
(4)定义:组距是每组观察值的最大差。 #
组距=某组上限值-该组下限值
极差
组数
第五步,确定组限。
#
|
下限 #
|
一个组的最小值 # |
|
上限 #
|
一个组的最大值 # |
|
组距 # |
上限与下限的差值 #
|
|
组中值 # |
上限值与下限值的平均值 # |
确定组限时应注意的问题
第一,第一组的下限值应比最小的观察值小一点,最后一组的上限值应比最大的观察值大一点。
第二,特别需要或不得已的情况除外,最好不要使用开口组。 #
第三,组限应取得美观些,按数字偏好,组限值应能被5除尽,且一般要用整数表示。 #
第六步,确定各组观察值出现的频数。 #
采用组距分组时,需要遵循“不重不漏”的原则。
【例如】“60~70”、“70~80”
70这个数字应划到“70~80”组里。 #
第七步,制作频数分布表,并填上相关的内容,以及其他需要说明的事项。
|
观察值区间 # |
组中值 # |
频数 # |
频率(%) # |
|
50-60 # |
55 # |
6 # |
10.9 # |
|
60-70 # |
65 #
|
7 #
|
12.7 #
|
|
70-80 # |
75 #
|
11 #
|
20.0 # |
|
80-90 # |
85 # |
13 # |
23.6 # |
|
90-100 # |
95 # |
13 #
|
23.6 # |
|
100-110 # |
105 # |
3 # |
5.5 # |
|
110-120 # |
115 #
|
2 # |
3.7 # |
|
合计 # |
— # |
55 # |
100.0 #
|
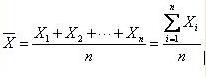
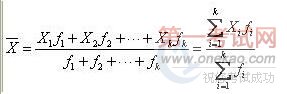




 京公网安备 11010802021846号
京公网安备 11010802021846号